I've just had a go at implementing Boids with Blender's Simulation Nodes (part of Geometry Nodes) and thought I would write up, briefly, the general process.
The quick idea of boids is that using three simple rules - Alignment, Cohesion, and Separation - you can get particles (or boids) to recreate the 'flocking' behaviour of birds or shoals of fish.
I followed along with The Coding Train's Coding Challenge #124 by Daniel Shiffman. Although the coding challenge is done in JavaScript, the process is mostly about adding or subtracting vectors, which is something that Geometry Nodes can do quite easily.
Detecting Neighbours
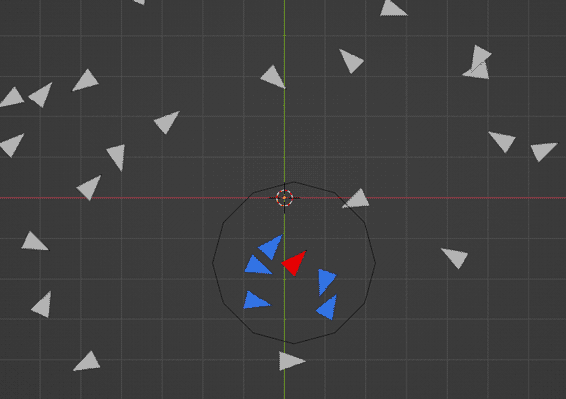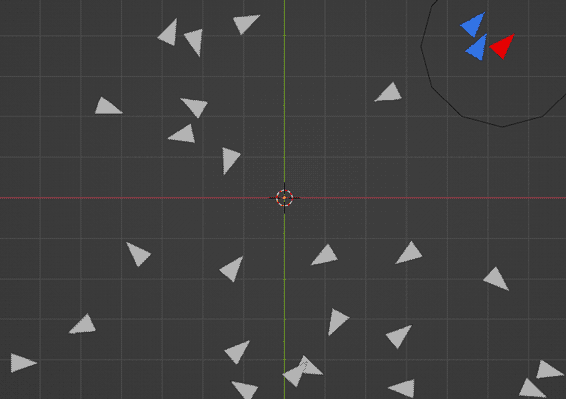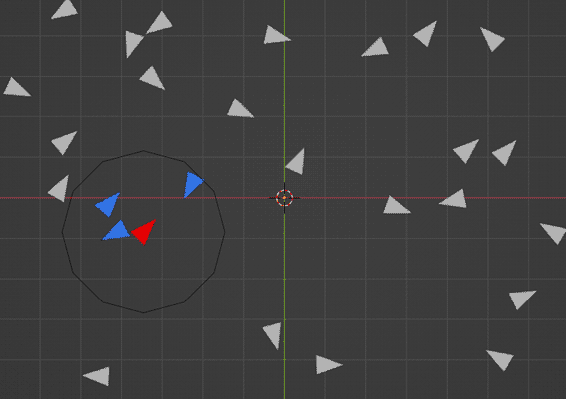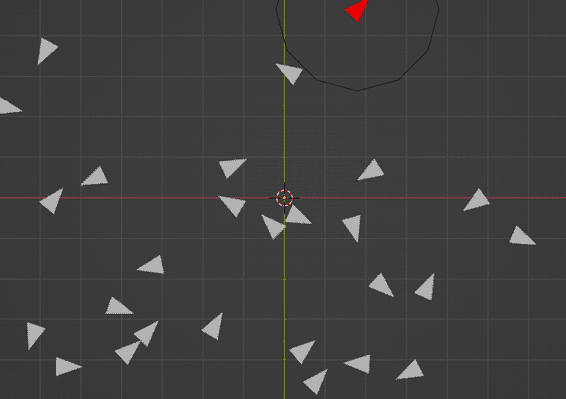
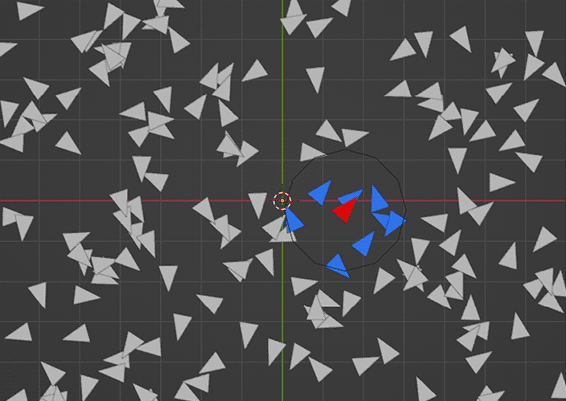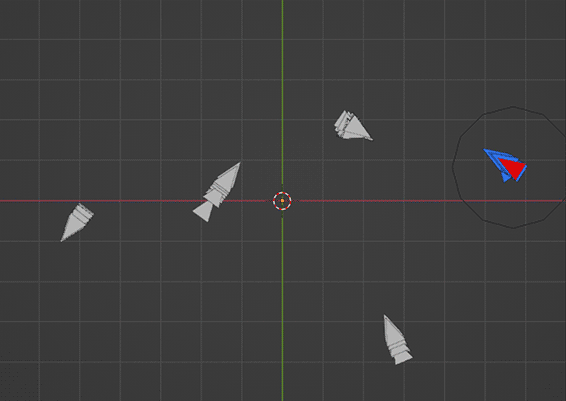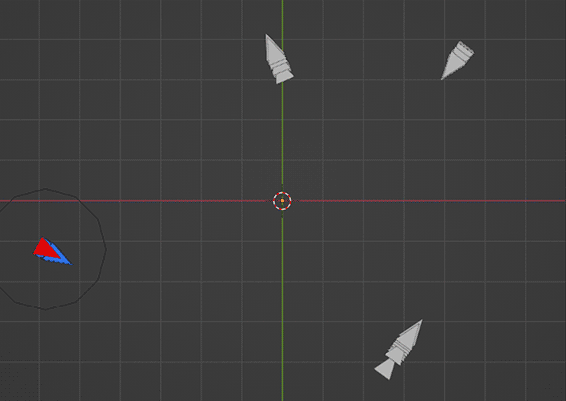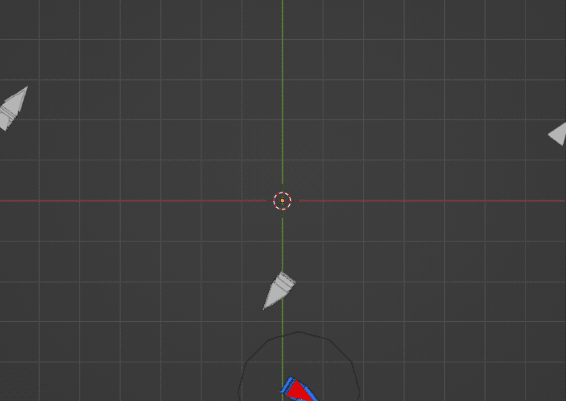
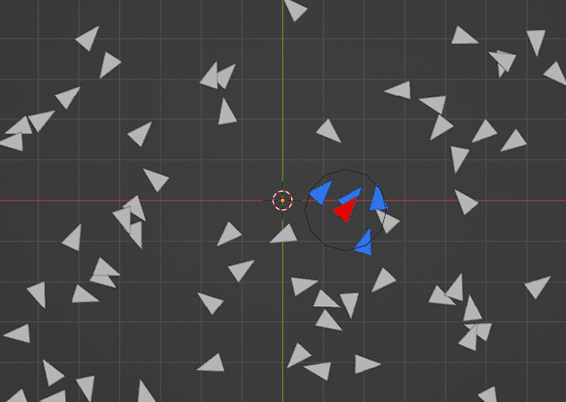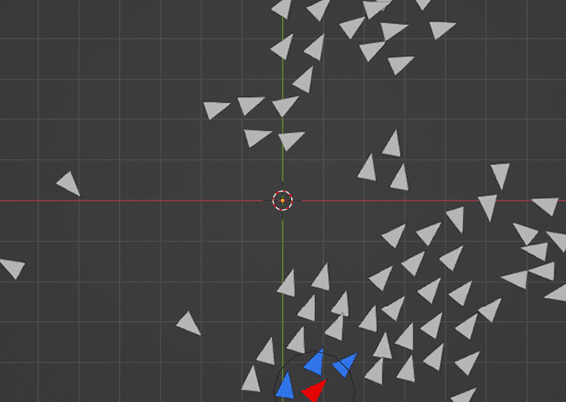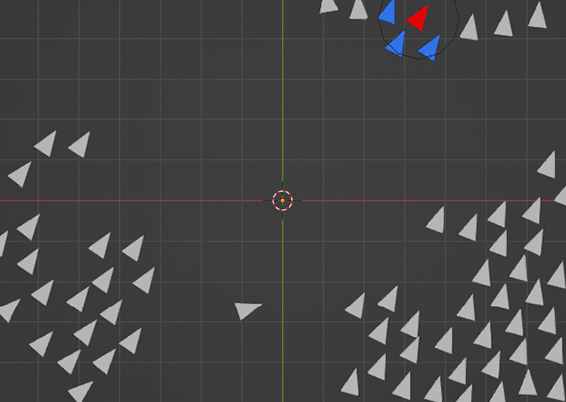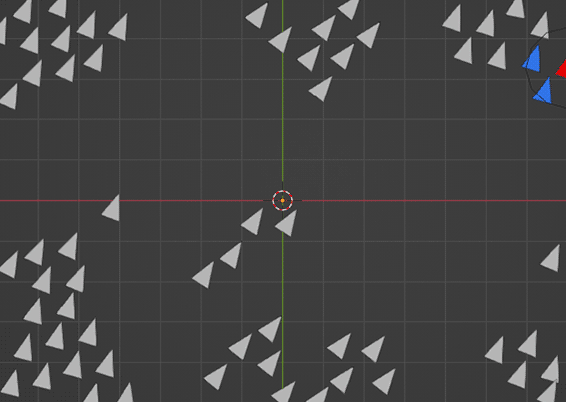
The first stage of getting any of this to work is for each boid to be able to detect its neighbours - the boids in a defined area around it. To begin with, I try just getting just one boid to detect the boids nearby.
The basic process of getting particles to even move is:
- Distribute points on faces (I used a plane)
- Store a 'velocity' attrbute
- Add a random vector to the velocity at the beginning of the simulation
- Add the velocity to itself each frame in the 'Simulation Zone'
- Set the position of the boids to be the velocity
After the Simulation Zone, I instance a triangle on the points and use the 'Align Euler to Vector' node with the velocity attribute plugged into its 'Vector' input for the rotation. This gets the triangles to point in the right direction.
I also make the points 'wrap' i.e., when they reach the edge of the rectangle they warp to the other side. This is done by comparing each of the position attrbute's individual axis to see whether they exceed the defined bounds, and if they do, set their position to the other side of the bounds.
Alignment
This is the part where boids should point, and therefore travel, in the direction of the neighbouring boids. To get this to work for all boids I used a Repeat Zone in a Simulation Zone, because every boid has to look at every other boid, like a nested loop. I keep thinking the Repeat Zone can be removed, but this was the most direct way of translating the code version of this.
To get the neighbours I first get the current boid by deleting everything apart from the current boid (this is the part that requires the Repeat Zone, which I'm not sure I need to do), plug it into a 'Geometry Proximity' node and then using a 'Compare' node I see if it's less than my desired neighbour radius (which is up to you). You can then use this selection to delete all points but the neighbours. All this is done in a 'Repeat Zone' set to run for the number of boid points that were initially generated.
Having got the neighbours, I used an Attrbute Statistic node to get the mean velocity of them and add that to the current boid's velocity.
Here's a simplified screenshot showing the general setup:
And here's the result:
Sometimes if two boid neighbours are pointing in opposite directions the average velocity will equal zero, causing the current boid to completely stop. To counter this, I give the boids a minimum speed by normalising and then scaling the velocity by a fixed amount. It is this fixed amount that actually becomes the velocity and so the previous velocity calculations really just end up changing the direction the boid moves in.
Cohesion
In the 'Cohesion' step the boids are not just meant to align with their neighbours, but move toward the centre of them. Visually this is less interesting because it just means the boids kind of pile on top of each other.
This also uses the mean but this time of the position attrbute. I found I had to subtract this from the velocity, which I think differs from the coding challenge, which adds it, but it gets the desired result so 🤷♂️.
Separation
Separation is a bit more complex and really it sounds like the reverse of cohesion, as now the boids are meant to move away from each other, which doesn't make sense. They're not meant to fully separate though, just organise themselves nicely, like birds flying in a formation.
Separation requires looking at the distance of the neighbouring boids. I use the Geometry Proximity for this. I subtract the position of the neighbour boid from the current one, divide it by the square of the distance beteen them, average them and then add it to the velocity. It sounds complex, and looking at the nodes makes me think I've got something wrong, but basically, the squaring and dividing means that out of the neighbours, the closest ones have the most effect. I think. As an additional step, multiplying the distance before squaring causes the separation to be larger or smaller, which can create very different effects.
And with the separation stage done, that's boids 'complete'! I say 'complete' because it could do with some optimisations for larger flocks and other features and finding out whether I actually need the Repeat Zone at all.
I did actually add one more 'feature', I converted it to a 3D simulation, which really didn't take much work aside from adapting the boid wrapping to take into account the Z axis as well.
I did then try implementing obstacles but only had minor success so I didn't include that.
I think I will leave it like this for the minute and maybe return to it later.
Ray.